Capítulo 2: Componentes lógicos: Representación de la información
Codificación de la información
Una vez que hemos comprendido la necesidad de representar la información que debe manejar un ordenador, convirtiéndola en un formato binario, y que hemos adquirido las habilidades básicas del manejo de ese sistema de numeración y su relación que el resto, llega el momento de poner el foco sobre el modo en el que se codifica la información dentro del ordenador.
Lógicamente, la forma de codificar la información dependerá de su propia naturaleza. No se codificará igual un texto, un valor entero u otro con parte decimal. A continuación, veremos los más básicos.
Codificación de caracteres
Como podemos deducir de todo lo que hemos dicho hasta el momento en este apartado, dentro de un ordenador todo son números. Por lo tanto, si queremos representar textos, necesitaremos establecer una correlación entre un valor entero y un carácter asociado a ese valor.
De esta forma, obtendremos una tabla donde cada carácter que queremos representar tiene asociado un valor numérico en binario. A esta tabla la llamaremos juego de caracteres.
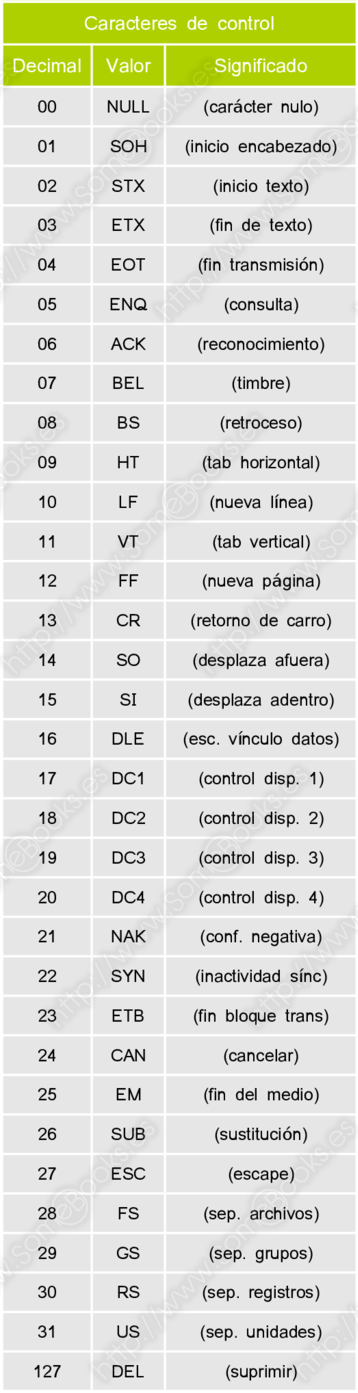
Además de los caracteres habituales, un juego de caracteres incluye caracteres de control que producen determinados efectos cuando se muestran en un dispositivo de salida (por ejemplo, avanzar a la línea siguiente). Estos caracteres de control pueden que no resulten muy importantes en la actualidad pero, en los primeros ordenadores, eran fundamentales para mostrar información impresa o en los terminales de texto.
Los juegos de caracteres de los primeros ordenadores, dada su escasa capacidad, trataban de utilizar el menor número posible de bits para representar cada carácter. Por ejemplo, FIELDATA usaba sólo 6 bits, lo que hacía que sólo pudieran representarse 64 caracteres diferentes (26=64), que incluían únicamente las letras del idioma inglés, en mayúsculas, los números decimales y unos cuantos símbolos de puntuación y matemáticos.
En 1963, el Comité Estadounidense de Estándares creó un juego de caracteres llamado ASCII (del inglés, American Standard Code for Information Interchange). Utilizaba 7 bits (27=128) y, además de las letras mayúsculas, caracteres de control y algunos otros caracteres especiales, incluía letras minúsculas.
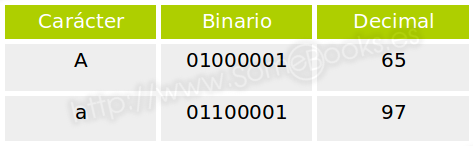
Una característica curiosa es que la representación de una letra en mayúsculas y en minúsculas sólo se diferencia en un bit, lo que hace que sea muy sencilla la conversión entre unas y otras. Veamos, a modo de ejemplo, la representación de la letra A en mayúscula y en minúscula:
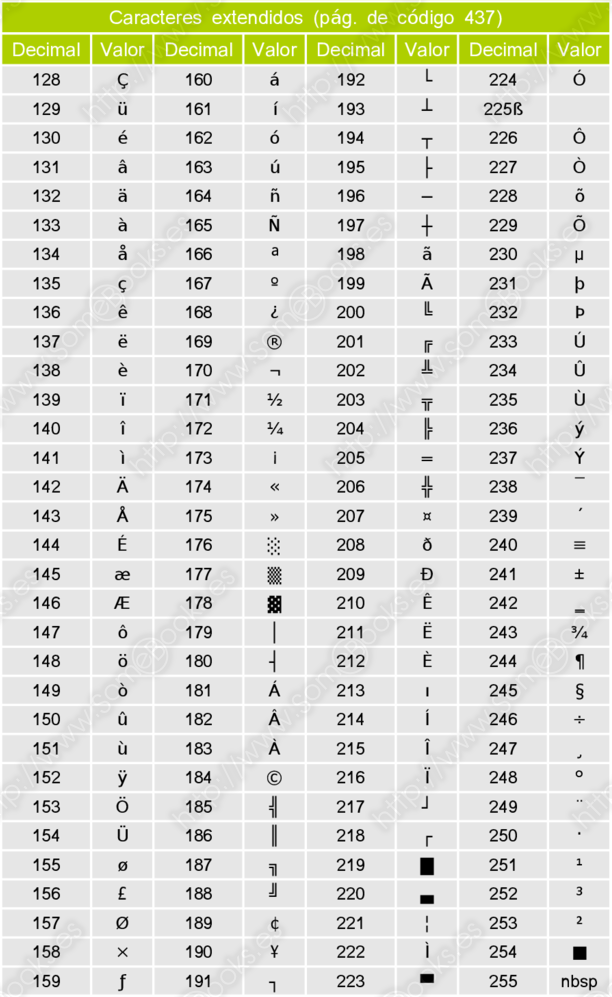
La variante de 8 bits suele llamarse ASCII extendido, o ASCII ampliado y, además de los caracteres propios de algunos idiomas occidentales (como nuestra ñ o la ç francesa) incluía caracteres semigráficos que, combinados, podían dar cierta ilusión de gráficos rudimentarios en monitores que sólo permitían representar texto.
A continuación, se incluye el mapa completo de caracteres ASCII ampliado dividido en tres bloques:
-
Caracteres de control
-
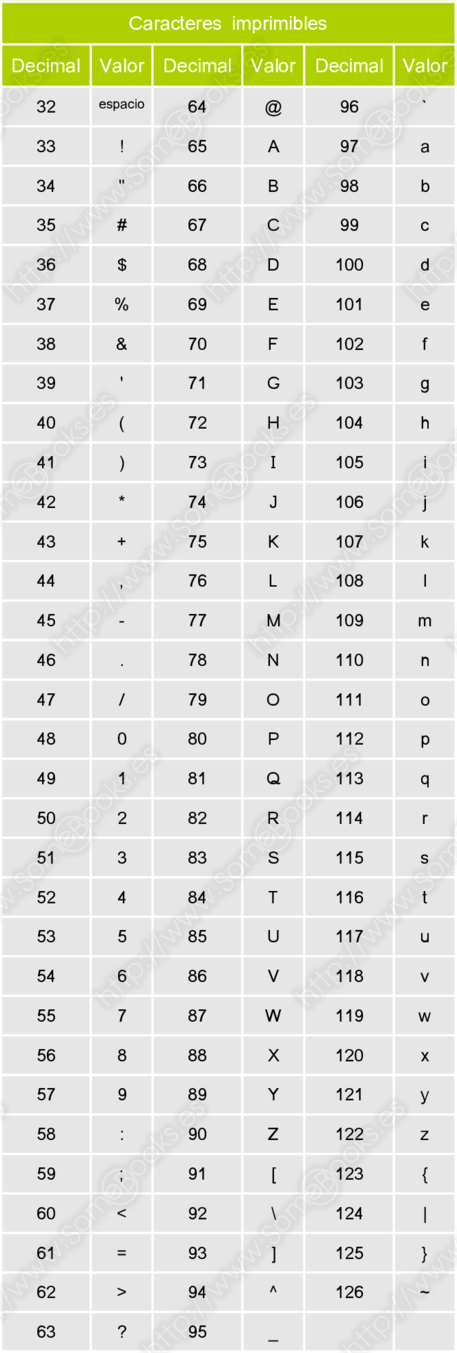
Caracteres imprimibles
-
Caracteres extendidos
Como puede comprenderse fácilmente, ASCII estaba pensado para satisfacer las necesidades de los idiomas occidentales, pero dejaba fuera cualquier otro que estuviese basado en caracteres diferentes (griego, árabe, ruso, chino, …). Tampoco es adecuado para la representación de textos en lenguas clásicas ni para la utilización de símbolos científicos.
Las primeras soluciones consistieron en crear variantes locales de los juegos de caracteres donde un mismo valor podía representar diferentes caracteres según la variante que usáramos. Estas variantes acabaron incluyéndose en una norma llamada ISO 8859 que tiene 16 variantes distintas. Por ejemplo, la norma ISO 8859-1 incluye caracteres de los idiomas usados en América, Europa occidental y Oceanía (incluido el español.
La siguiente tabla incluye los 16 alfabetos ISO 8859 definidos hasta la fecha:
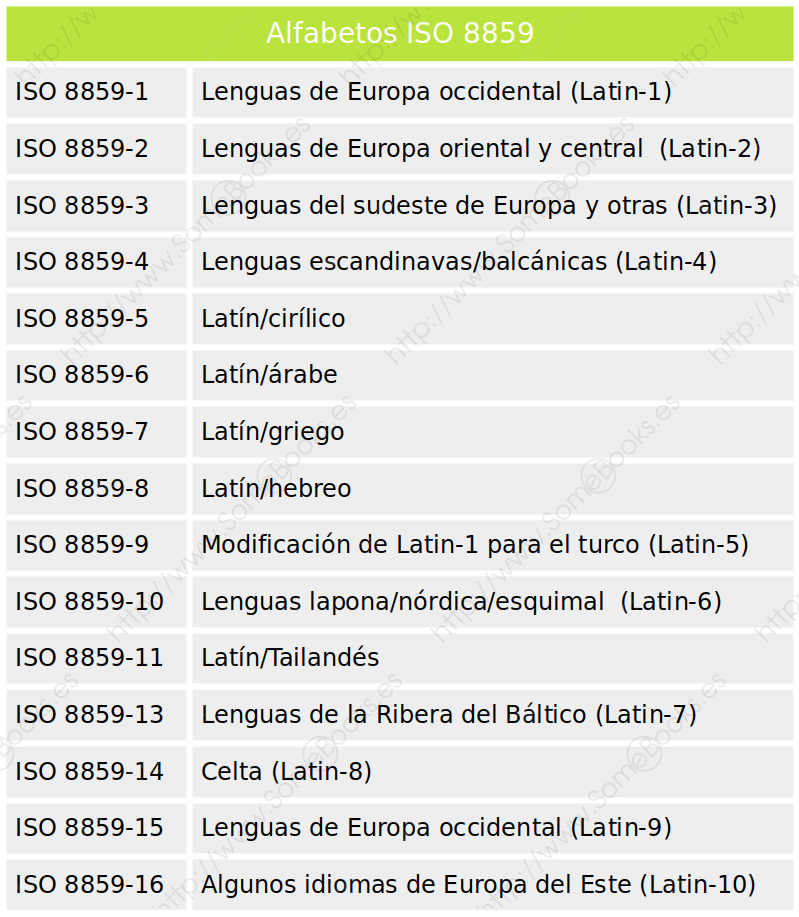
Puedes obtener el conjunto de caracteres completo para la variante ISO 8859-1 en el siguiente enlace: https://www.charset.org/charsets/iso-8859-1
… Y para el resto de los alfabetos, basta con cambiar el último número de la URL.
Sin embargo, esto podía ocasionar problemas, sobre todo en sistemas servidores o cuando varios ordenadores compartían información entre ellos. Además, resultaba imposible utilizar varios idiomas al mismo tiempo, si no estaban soportados por la misma variante.
Para resolver este tipo de situaciones, varios ingenieros de Apple y Xerox propusieron en 1988 un nuevo estándar de codificación de caracteres al que se llamó Unicode (el primer borrador recibió el nombre de Unicode88 y utilizaba 16 bits para representar caracteres). Sin embargo, el Consorcio Unicode no se constituyó hasta 1991.
En la actualidad, se trata del esquema de representación de caracteres más completo y permite que los ordenadores se adapten al modo en el que se representa el texto en prácticamente todos los idiomas del planeta.
Comprende tres codificaciones diferentes:
-
UTF-8: Es la forma más frecuente de codificación Unicode. Utiliza 8 bits para codificar letras y símbolos en idioma inglés, 16 bits para codificar caracteres latinos y de Oriente Medio, y 24 bits para idiomas asiáticos. Incluso puede llegar a utilizar 32 bits para representar caracteres adicionales.
Los primeros 128 caracteres coinciden con ASCII, por lo que son compatibles.
-
UTF-16: Utiliza 16 bits, lo que le permite representar hasta 65,536 caracteres diferentes. Ocasionalmente, puede utilizar 32 bits (de los que 11 se mantienen siempre a cero) para llegar a representar 1,112,064 de caracteres y símbolos distintos.
-
UTF-32: A diferencia de los anteriores, que pueden utilizar longitudes variables, aquí se utilizan siembre 32 bits para representar cada carácter… Aunque en realidad solo utiliza 21 (de nuevo, 11 quedan siempre inutilizados).
A pesar de que ocupa más espacio, su velocidad es mayor, porque no habrá que calcular el número de bits que se utilizan en cada momento.
UTF son las siglas, en inglés de Unicode Transformation Format.
Una de las mayores ventajas de Unicode es que ofrece un mismo valor numérico para cada uno de los caracteres, de forma independiente del hardware, del software y del idioma que se estén utilizando. Esto permite que programas y sitios web se adapten fácilmente a diferentes contextos de uso de forma sencilla y que los datos puedan compartirse entre sistemas diferentes sin verse alterados.
Hoy en día, Unicode ha sido asumida por la mayoría de las empresas líderes de la industria informática (como Microsoft, Apple, Oracle, IBM, etc.) y por casi todos los estándares actuales (como LDAP, XML, Java, etc).
Si quieres consultar todos los esquemas disponibles, puedes recurrir a la página http://www.unicode.org/charts/. Por ejemplo, en la siguiente imagen podemos ver la
representación de los símbolos que configuran el sistema Braille: 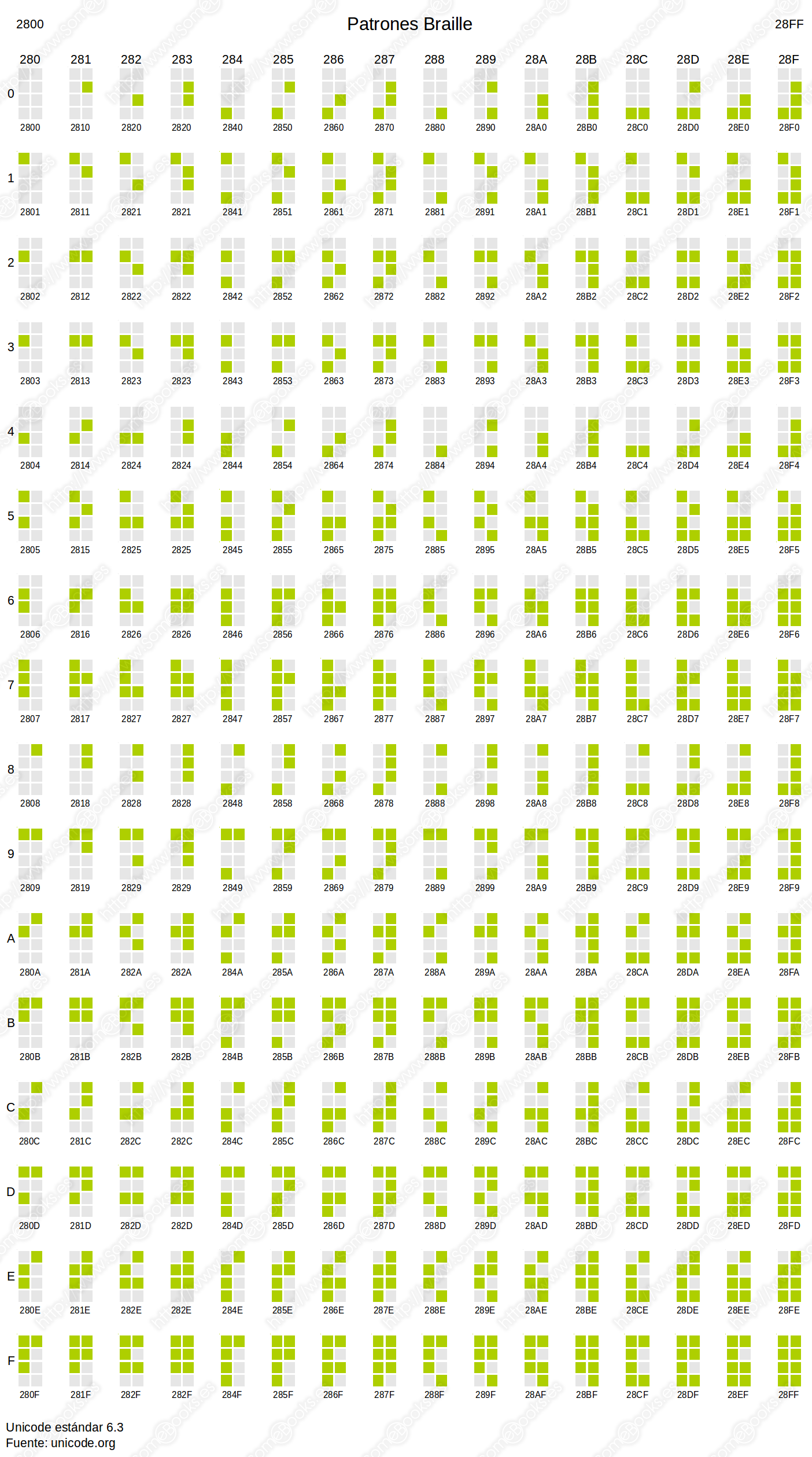
Codificación de valores numéricos
Con todo lo dicho hasta ahora, podríamos pensar que representar números dentro de un ordenador es más sencillo. Sin embargo, el método a seguir dependerá de la naturaleza de los valores a codificar. No podremos utilizar las mismas técnicas para codificar los números naturales, los enteros o los racionales.
Sin embargo, el objetivo siempre será doble:
-
Maximizar el rango de valores que puede representarse.
-
Facilitar la realización de operaciones con ellos.
Codificar números naturales
Como recordarás de la asignatura de matemáticas, los números naturales son enteros y positivos, lo que significa que para representarlos dentro del ordenador no necesitaremos representar ni el signo ni el punto decimal.
Por lo tanto, el rango de valores admitido estará en función, únicamente, del número de bits que utilicemos.
Ya hemos visto más arriba que si tenemos, por ejemplo, 8 bits podremos representar 256 valores diferentes: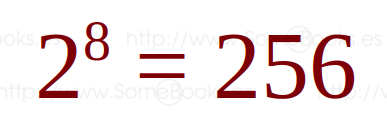
Esto nos permitirá representar un intervalo de valores que van desde 0 hasta 255 (00000000 a 11111111).
De forma genérica podemos decir que, si tenemos n bits, el mayor número natural que podemos representar con ellos será: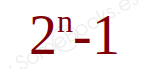
Codificar números enteros
Para representar un número negativo en matemáticas, sólo tenemos que hacer algo tan fácil como escribir un guión delante de la cantidad. Sin embargo, este fue el primer problema al que se enfrentaron los primeros diseñadores de ordenadores, ya que ahora debemos reservar un bit para representar el valor del signo.
Existen varios enfoques a este problema:
-
Módulo-signo, también conocido por signo-magnitud.
-
Complemento a uno, también llamado complemento a la base menos uno.
-
Complemento a dos, también llamado complemento a la base.
-
En exceso a N.
Para entender cómo funciona cada una de estos modos de representación a continuación se incluyen algunos detalles más:
Módulo y signo (MS)
Este es el modo más sencillo para representar en binario un número entero con signo. La idea es que, si partimos de un número fijo de bits (8, 16, 32, …), se reserva el primero de ellos (el que hay más a la izquierda), para representar el signo. El resto representarán el valor absoluto del número en binario.

Por lo tanto, su rango de valores podríamos representarlo con la siguiente expresión, donde X representa el valor y n el número total de dígitos que usaremos para representarlo, incluido el signo:
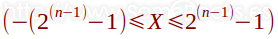
Así, por ejemplo, si utilizamos 8 dígitos binarios, sólo usamos 7 para el valor absoluto. Dado que el número máximo de combinaciones posibles con 7 bits es de 128 (27), los posibles valores que podremos representar se encontrarán entre 0 y 127.
Por lo tanto, si tenemos en cuenta el signo, el rango de valores que podremos representar con 8 bits mediante representación en módulo y signo estará entre -127 y 127.
Veamos algunos ejemplos:
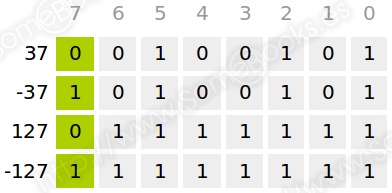
En la siguiente tabla mostramos los rangos de valores para algunos tamaños de palabra frecuentes:
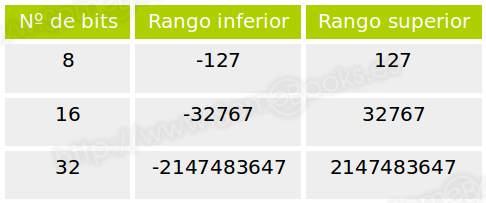
Aunque se trata de un modo muy evidente de representación numérica, tiene dos inconvenientes: La primera, y menos importantes es que la representación del valor cero es doble (0 y -0). La segunda es que resulta complicado usarla en operaciones aritméticas.
Complemento a uno (C-1)
Como en el caso anterior, su objetivo es representar números enteros, tanto positivos como negativos. Además, también en este caso se utiliza el primer bit para representar el signo.
Como en módulo y signo, los números positivos se representan poniendo a cero (positivo) el primer bit, usando el resto para representar el valor absoluto del número en binario.
Sin embargo, un valor negativo se representa complementando el valor positivo correspondiente. Es decir, invirtiendo el valor de todos los bits del número positivo, incluido el que representa al signo.
Veamos algunos ejemplos usando una representación de 8 bits:
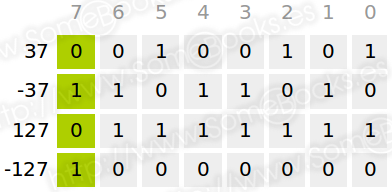
Como habrás deducido, el rango de valores posibles para un determinado número de bits es idéntico al obtenido en módulo y signo. Además, también aquí la representación de valor cero es doble. Por ejemplo, utilizando 8 bits, podríamos representarlo como 00000000 (0) y 11111111 (-0).
Tampoco suele emplearse para realizar operaciones aritméticas.
Complemento a dos (C-2)
La representación en Complemento a dos es idéntica a la que hemos aplicado en complemento a uno, pero sumando después el valor 1 a los números negativos. Si en esta suma se produce acarreo, deberemos despreciarlo.
Veamos algunos ejemplos representando valores en complemento a uno y en complemento a dos usando una representación de 8 bits:
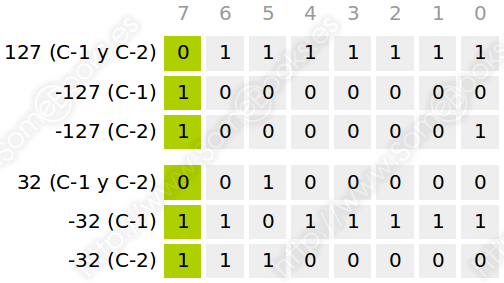
En esta situación, cabría preguntarse qué ocurre cuando representamos 0 partiendo de la segunda representación de complemento a 1 (11111111), es decir, partiendo de la representación negativa. Como puedes ver en la siguiente tabla, al sumar 1, todos los bits quedarían a cero, obteniendo al final un acarreo de 1 que se despreciaría.
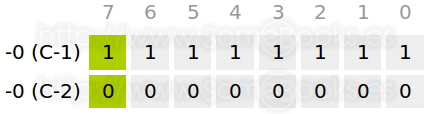
En definitiva, llegamos a la conclusión de que sólo existe una representación del valor 0, lo que implica también disponer de un valor negativo más en el rango y, por consiguiente, un rango asimétrico:
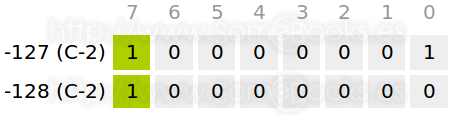
Por lo tanto, su rango de valores podríamos representarlo son la siguiente expresión, donde X representa el valor y n el número total de dígitos que usaremos para representarlo, incluido el signo:
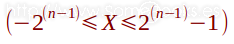
En la siguiente tabla mostramos los rangos de valores para algunos tamaños de palabra frecuentes:
A diferencia de los casos anteriores, la representación en complemento a dos si es muy utilizada para operaciones aritméticas con números enteros. Y para ilustrarlo, pondremos algunos ejemplos.
Suma en complemento a dos
La suma se realiza de la forma habitual, sin tener en cuenta si los números son positivos o negativos.
El único inconveniente puede producirse cuando sumamos valores con el mismo signo (dos valores positivos o dos valores negativos. En estos casos, puede ocurrir que el resultado obtenido sobrepase los límites del rango que ofrezca el número de bits que estemos empleando.
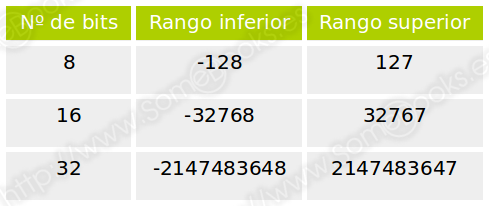
Por ejemplo, esto ocurriría si, utilizando una representación de 8 bits, sumáramos los valores 96 y 37. En principio, podremos representar, de forma correcta, ambos valores en complemento a dos. Sin embargo, al sumarlos, el resultado arrojaría el valor 133, que excede el valor máximo representable (que es 127).
Si ocurre esto cuando un ordenador trata de realizar una operación, se obtiene un error de desbordamiento (en inglés, overflow).
Cuando los sumandos tienen el mismo signo, detectaremos que se ha producido un desbordamiento cuando el resultado tiene un signo diferente.
Por ejemplo, si realizamos la suma anterior, el resultado sería este:
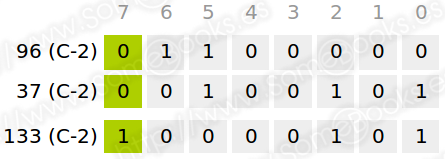
Y si lo intentamos con números negativos…
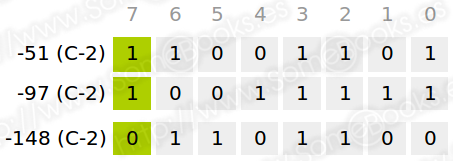
En este caso, hemos despreciado el último acarreo.
Resta en Complemento a dos
Para restar dos números en complemento a dos, basta con volver a calcular el complemento a 2 del sustraendo (lo que equivale a cambiarlo de signo) y realizar la suma con el método explicado más arriba.
Para comprobarlo, vamos a restar dos números con los que hemos trabajado antes: 96 y 37.
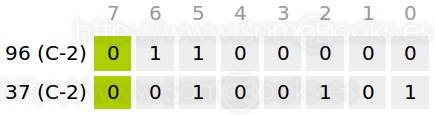
Lo primero será cambiar el signo de 37 en complemento a dos:

A continuación, realizamos la suma:
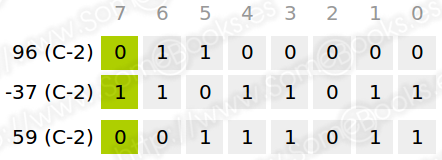
La importancia de este funcionamiento radica en que los ordenadores que representen los valores enteros en complemento a dos sólo necesitarán un circuito sumador para realizar tanto sumas como restas. Por otro lado, los circuitos que complementan valores binarios son muy sencillos de implementar.
Exceso a 2n-1.
En este caso, antes de representar cada valor, se le suma el resultado de calcular 2n-1, donde n representa el número de dígitos utilizados para la representación. Es decir, si vamos a representar valores usando 8 bits, a cada valor a representar debemos sumarle 128 (27). A continuación, hacemos la conversión a binario sin tener en cuenta el signo.
Veamos algunos ejemplos usando una representación de 8 bits:
- Ejemplo 1: el valor 37.
- Como hemos dicho, lo primero será sumarle 128. El resultado es 165.
- A continuación, convertimos 165 en binario puro. El resultado es:

- Ejemplo 2: el valor -37.
- Como antes, lo primero será sumarle 128. El resultado es 91.
- Si ahora convertimos 91 a binario puro, obtenemos:

- Ejemplo 3: el valor 0.
- De nuevo, comenzamos sumando 128, aunque, en este caso, el resultado es 128.
- A continuación, convertimos 128 en binario puro. El resultado es:

Si seguimos haciendo pruebas, comprobaremos que el bit 7 de todos los números positivos acabará siendo 1. Y el de los números negativos será 0. Además, comprobamos que el valor cero se representa en el intervalo de números positivos, de lo que se desprende que el rango de representación es asimétrico (como nos ocurría en complemento a dos), pudiendo representarlo con la siguiente expresión, donde X representa el valor y n el número total de dígitos que usaremos para representarlo:
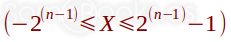
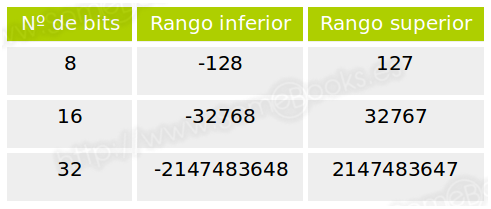
En la siguiente tabla mostramos los rangos de representación para algunos tamaños de palabra frecuentes:
Codificar números racionales
Cuando se trata de representar números con decimales, los tipos de representación más frecuentes son estos:
-
Decimal codificado en binario o BCD (del inglés, Binary-Coded Decimal).
-
Decimal desempaquetado.
-
Decimal empaquetado.
-
Coma flotante.
A continuación, vamos a incluir una explicación más detallada de los sistemas de representación de números decimales mencionados más arriba.
Codificar usando BCD
La representación en BCD asigna 4 bits para representar en binario cada uno de los dígitos de un número decimal. Así, por ejemplo, el número 1 podría representarse como 0001. Siguiendo esta idea general, suelen aplicarse distintos modos de representación. En la siguiente tabla mostramos los más frecuentes:
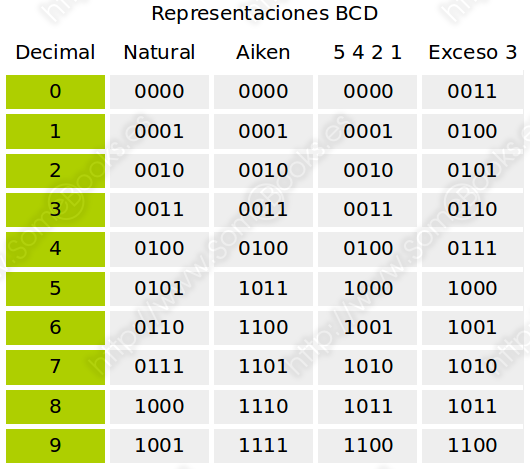
Aunque el método es indiferente de la representación concreta que utilicemos, para esta documentación, utilizaremos la representación Natural.
Observa que, a pesar de que, con cuatro bits, podríamos representar hasta quince valores, en BCD siempre se desprecian seis de ellos.
Cuando el número decimal que queremos representar con BCD tiene más de un dígito, se usan tantos grupos de cuatro dígitos binarios como dígitos decimales tenga el número de origen. Como dicho así puede resultar algo lioso, veamos el siguiente ejemplo:

La ventaja que ofrece BCD es que evita la pérdida de exactitud producida por las conversiones de decimal a binario y viceversa.
Por contra, el inconveniente es que los cálculos con números representados en BCD son más complejos y, por consiguiente, emplean más tiempo de proceso.
Decimal desempaquetado
La representación en Decimal desempaquetado trata de suplir una de las carencias de BCD: su imposibilidad de representar números negativos.
Para solventarlo, Decimal desempaquetado utiliza un byte para representar cada dígito decimal. El nibble de la derecha se corresponde con la representación en BCD, mientras que el nibble de la izquierda puede tener tres valores posibles:
- El valor 1111(2 en todos los dígitos excepto en el primero.
- El valor 1100(2 en el primer dígito, cuando el número es positivo.
- El valor 1101(2 en el primer dígito, cuando el número es negativo.
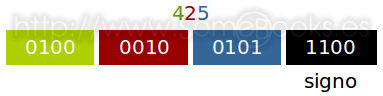
A modo de ejemplo, veamos la representación del número 425 que ya mostrábamos en BCD:

Y si el número fuese -425, quedaría así:

Este método facilita mucho la representación de los valores, ya que utiliza un byte binario para cada dígito decimal. Sin embargo, conlleva el uso de un gran número de bits innecesarios. Piensa que, con cada byte podemos representar 256 valores diferentes, de los que sólo se utilizan 10 para cada dígito decimal (20 en el caso del primero).
Decimal empaquetado
Resuelve los inconvenientes del sistema decimal desempaquetado ya que elimina el nibble de la izquierda para cada dígito, salvo el primero. De esta forma, se pueden representar dos dígitos decimales en cada byte (por ese motivo se le llama empaquetado).
El signo siempre se representa en el nibble de la derecha del byte más a la derecha.
Cuando se trata de representar números muy grandes, o muy pequeños, se utiliza la representación en coma flotante, que está basada en la notación científica utilizada habitualmente en matemáticas.
La notación científica consiste en representar las cantidades en función de una potencia de 10. Así, el número 6.400.000 se representaría como 6,4 x 106, mientras que el número 64.000.000 se representaría como 6,4 x 107.
En informática, normalmente se utilizan 32 bits (simple precisión) o 64 bits (doble precisión) para representar cada número en coma flotante.
La representación de números enteros no es adecuada para un gran número de situaciones. En algunos casos, podríamos utilizar parte de los dígitos para representar valores decimales, pero estaríamos reduciendo el rango de valores representables.
Para entender la idea, podemos pensar en la representación en complemento a 2, utilizando 32 bits. En condiciones normales, el rango de representación iría desde -2.147.483.648 hasta 2.147.483.647. Sin embargo, si reserváramos los dos últimos dígitos para representar valores decimales, el rango de representación se reduciría desde -21.474.836,48 hasta 21.474.836,47. Imagina lo que ocurrirá cuando necesitemos una mayor precisión decimal.
Podríamos pensar que la solución está en aumentar el número de bits que utilizamos en la representación (pasar de 32 a 64, o a 128). Sin embargo incluso en ese caso, podemos encontrarnos, sobre todo en el ámbito científico, con cálculos que necesiten manejar valores extraordinariamente grandes o extraordinariamente pequeños.
Para resolver esta situación, en el campo de las matemáticas se utiliza notación científica, que consiste en representar las cantidades en función de una potencia de 10. Así, por ejemplo, para representar la distancia más grande que podemos observar en el universo, que es de 740.000.000.000.000.000.000.000.000 metros, podemos utilizar la expresión 7,4 x 1026 que, como puedes ver, resulta mucho más manejable.
Recuerda: 1 gúgol, que es el origen del nombre Google, equivale a 10.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000 unidades, pero podemos representarlo, cómodamente, como 10100.
Lo mismo ocurre con valores muy pequeños. Por ejemplo, la masa de un electrón es de 0,00000000000000000000000000000091 Kg, pero podemos representarlo como 9,1 x 10-31.
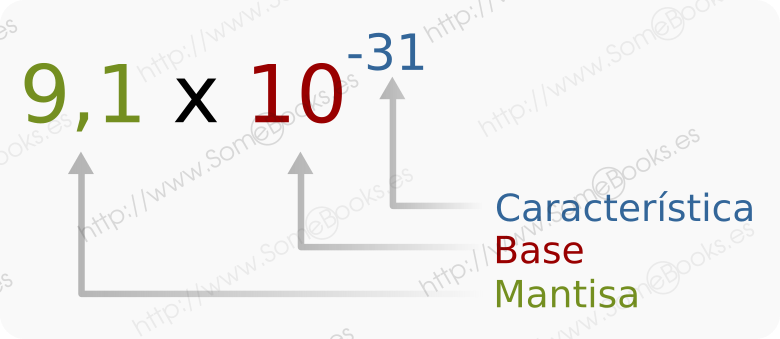
A esta forma de notación se le llama representación en coma flotante. En ella, podemos diferenciar tres elementos:
- La mantisa: Es el primer número de la expresión.
- La base: Representa el sistema de numeración en el que estamos trabajando. En matemáticas siempre es 10.
- La característica: Es el exponente al que debe elevarse la base
Cómo se utiliza representación en coma flotante en un ordenador.
Lo primero que debemos contemplar cuando pretendemos representar un número en coma flotante dentro de un ordenador es que, en lugar de utilizar base 10, emplearemos base 2. Además, deben seguirse las siguientes pautas del IEEE:
- El signo debe representarse con un solo bit (0 = positivo y 1 = negativo).
- La característica se representará mediante exceso a 2N-1-1. Es decir, en el caso de que el número de bits a utilizar sea 8, al exponente le sumaremos 127 (28-1-1 = 127) para almacenarlo. El motivo es que, al manejar todos los valores como positivos, se simplifican algunas operaciones. Además, sólo se utiliza el rango 1 a 254, porque se le otorga un significado especial a 0 (00000000(2) y a 255 (11111111(2).
- La mantisa se normaliza para situar la coma detrás del primer dígito que sea igual a 1 por la izquierda (por ejemplo: 1,100101). Además, ese primer dígito puede darse por sobreentendido, lo que permite no representarlo y aumentar la precisión en un bit.
- La base, que siempre es 2, también se da por sobreentendida y no se representa.
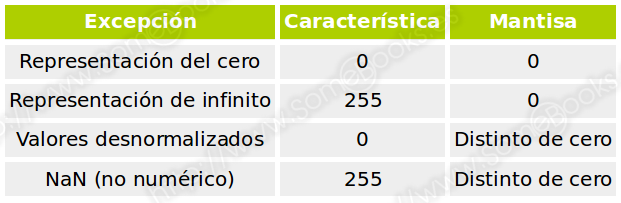
A esta norma se le plantea una excepción evidente: el valor cero debe poder representarse, pero la mantisa nunca tendrá un 1 tras el que situar la coma. Para resolverlo, se estableció que el valor cero se representaría con los bits de característica y mantisa a cero. Además de ésta, también se contemplan otras excepciones que se describen en la siguiente tabla:
La norma IEEE754 establece dos formas diferentes de representación:
- Utilizando 32 bits, que recibe el nombre de simple precisión, donde se utiliza 1 bit para el signo, 8 bits para la característica y 23 bits para la mantisa.
- Utilizando 64 bits, que recibe el nombre de doble precisión, en la que se utiliza 1 bit para el signo, 11 bits para la característica y 52 bits para la mantisa.
El IEEE (Institute of Electrical and Electronic Engineering) es un organismo de ámbito mundial encargado de desarrollar estándares relacionados con la tecnología.
Aún así, hay fabricantes que añadan sus propias representaciones, como la precisión ampliada de IBM, que utiliza 128 bits.
A modo de ejemplo, representaremos el número 9512(10 en coma flotante. Para lograrlo, seguiremos el siguiente proceso:
-
Primero lo convertimos en binario: El resultado es 10010100101000(2.
-
A continuación, movemos la coma 13 posiciones a la izquierda y, para dejar el valor constante, multiplicamos por la potencia correspondiente: 1,0010100101000(2 x 213(10.
-
Después, comenzamos la representación:
-
Como el número es positivo, el primer bit será 0.
-
La característica la representamos como 13 + 127 (140) en binario: 10001100
-
La mantisa estará formada por los dígitos que aparecen después de la coma, completando por la derecha con tantos ceros como sean necesarios para completar los 23 dígitos que debe ocupar la mantisa. Es decir: 00101001010000000000000
-
Por lo tanto, la representación quedaría así:
Aunque es muy común utilizar la notación en hexadecimal para que resulte más manejable. Para lograrlo, sólo tenemos que agrupar los dígitos de cuatro en cuatro y buscar su equivalencia. Para el ejemplo anterior, el resultado sería este:
4614A000(16
Como estamos utilizando un bit para el signo, tendremos dos rangos de representación: uno para los números positivos y otro para los números negativos.
Para averiguar cuáles son esos rangos de valores, debemos pensar en cuál es el valor mínimo y el valor máximo de la característica y de la mantisa. Pondremos como ejemplo la simple precisión:
- Para la característica:
- El valor mínimo es 1 (00000001(2), ya que el 0 es un valor excepcional. Como está representado en exceso a 127, el resultado será 1 – 127 = -126.
- El valor máximo es 254 (11111110(2), ya que el 255 es un valor excepcional. De nuevo, como se representa en exceso a 127, el resultado será 254 – 127 = 127.
- Para la mantisa:
- El valor mínimo será 1 seguido de una coma y 23 ceros (1,000…0(2). En definitiva, 1
- El valor máximo será 1 seguido de una coma y 23 unos (1,111…1(2), lo que es, prácticamente, 2 – 2-23, un valor bastante próximo a 2.
Así pues, los números negativos se encontrarán entre (-2+2-23) x 2127 y -1 x 2-126 mientras que los positivos estarán entre 1 x 2-126 y (2 – 2-23) x 2127.
Para la doble precisión podríamos hacer los mismos cálculos y obtendríamos que los números negativos se encontrarán entre (-2+2-52) x 21023 y -1 x 2-1022 mientras que los positivos estarán entre 1 x 2-1022 y (2 – 2-52) x 21023.
Otros tipos de codificaciones
Hasta ahora, hemos hablado del modo en el que un ordenador puede almacena los tipos de datos básicos. Sin embargo, existe una gran diversidad de información que se codifica y se manipula dentro de un ordenador. Veamos algunos ejemplos de los formatos de codificación más comunes:
- Para audio: mp3, wav, ogg, aiff, …
- Para vídeo: mpeg
- Para imágenes: jpeg, png, gif, tiff, …
El concepto de dato se puede definir como la representación simbólica de una propiedad relativa a una entidad. El concepto de información se define como un conjunto organizado de datos relativos a una entidad.